Reinforcement Learning as Probabilistic Inference - Part 2

Decision Making as a Probabilistic Graphical Model (PGMs)

Decision making problems (formalized as RL or optimal control), can be viewed as a generalized Probabilistic Graphical Model (PGM) augmented with utilities or rewards, that are viewed as extrinsic signals. PGMs are a mathematical framework for representing and reasoning about uncertain systems. It uses a graph-based representation as the basis for compactly encoding a complex distribution over a high-dimensional space. It turns out that graph as a representation of a set of independencies, and the graph as a skeleton for factorizing a distribution, are in a deep sense, equivalent! In this graphical representation, illustrated in the figure below, the nodes (or ovals) correspond to the variables in our domain, and the edges correspond to direct probabilistic interactions between them [1].

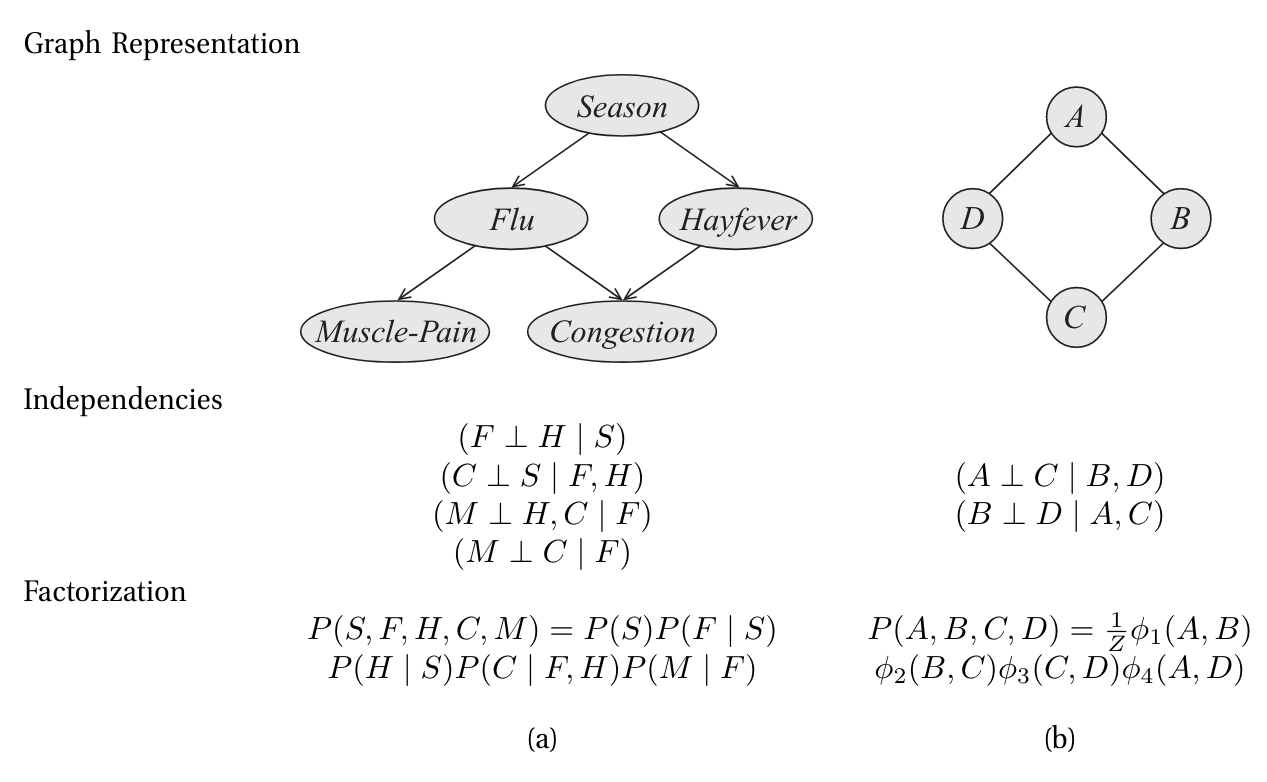
[1] describes two families of graphical representations of distributions; Bayesian networks represented with a directed acyclic graph and Markov networks, using undirected graphs. PGMs concisely represent independence properties and factorization structure of distributions.

Conditional interdependencies among variables are encoded as:

• D-separation in the directed graph for Bayesian networks.
• Separation in the undirected graph for Markov networks.

Factorization—how the joint probability distribution breaks into smaller, simpler components–—is explicitly represented as:

• Directed edges define the conditional probabilities in Bayesian networks.
• Cliques define the potential functions in Markov networks.

In the framework of PGMs, it is sufficient to write down the model and pose the question, and the objectives like parameter estimation, marginalization, or conditional probability computation arise directly from the graphical structure.

A common approach to solving decision making problems is to model the underlying dynamics as a probabilistic model e.g. with model-based RL, and determine an optimal plan or policy in a distinct process, e.g. trajectory optimization. In this frame, determining an optimal course of action or an optimal decision-making strategy (a policy) is considered a fundamentally distinct type of problem than probabilistic inference.

Reinforcement Learning $\leftrightarrow$ Trajectory Prediction

Is it possible to cast the decision making problem into an inference problem using a particular type of PGM? [2] claims is it possible to formulate these two so that they return the same results ; a trajectory following a policy that we get from solving the sequential decision making task with RL and an optimal trajectory from conditioning on a probabilistic model trained on trajectory prediction.

The Decision Making Problem - standard RL formulation

We will use $s \in S$ to denote states and $a \in A$ to denote actions, which may each be discrete or continuous. States evolve according to the stochastic dynamics $p(s_{t+1} \mid s_t, a_t)$, which are in general unknown.We will follow a discrete-time finite-horizon derivation, with horizon $T$, and omit discount factors for now. A task in this framework can be defined by a reward function $r(s_t, a_t)$. Solving a task typically involves recovering a policy $p(a_t \mid s_t, \theta)$, which specifies a distribution over actions conditioned on the state and parameterized by some parameter vector $\theta$.

A standard reinforcement learning policy search problem is then given by the following maximization:

$\theta^\star = \textcolor{blue}{\underbrace{\textcolor{black}{\arg\max_\theta}}_{\text{Vector of policy parameters}}} \textcolor{blue}{\underbrace{\textcolor{black}{\sum_{t=1}^T \mathbb{E}_{(s_t, a_t) \sim p(s_t, a_t \mid \theta)}\left[ r(s_t, a_t) \right]}}_{\text{Expected rewards over trajectories}}}$ We are trying to find the vector of policy parameters $\theta$ that maximize the expectation of reward $\sum_t r(s_t, a_t)$ with state and action taken according to the policy, for each step t=1 to T across the trajectory. Lets express the random variable in terms of a distribution of trajectories. Starting with:

$\sum_{t=1}^T \mathbb{E}_{(s_t, a_t) \sim p(s_t, a_t \mid \theta)} \left[ \dots \right],$

we can rewrite the expectation as a sum over all possible state-action pairs from $t = 1$ to $T$:

$\sum_{(s_1, a_1), \dots, (s_T, a_T)} p(s_1, a_1, \dots, s_T, a_T \mid \theta) \left[ \dots \right].$

Recognizing that the sequence $(s_1, a_1, \dots, s_T, a_T)$ represents a trajectory $\tau$, we can express this as:

$\sum_{\tau} p(\tau) \left[ \dots \right],$

where:

$\begin{aligned} p(\tau) &= p(s_1, a_1, \dots, s_T, a_T \mid \theta) \\ &= p(s_1) \prod_{t=1}^T \textcolor{blue}{\underbrace{\textcolor{black}{p(a_t \mid s_t, \theta)}}_{\text{Action likelihood}}} \textcolor{blue}{\underbrace{\textcolor{black}{p(s_{t+1} \mid s_t, a_t)}}_{\text{Transition likelihood}}}. \end{aligned}$

So this is the final expression we are trying to optimize in a standard reinforcement learning policy search problem :

$\theta^\star = \textcolor{blue}{\underbrace{\textcolor{black}{\arg\max_\theta}}_{\text{Vector of policy parameters}}} \textcolor{blue}{\underbrace{\textcolor{black}{\sum_{\tau} p(\tau) \left[ \sum_{t=1}^T r(s_t, a_t) \right]}}_{\text{Expected total reward over trajectories}}} \tag{1}$

Formulating the Decision-Making PGM

The next question we have to ask how can we formulate a probabilistic graphical model such that inferring the posterior action conditional $p(a_t \mid s_t, \theta)$ gives us the optimal policy?

We have to introduce an additional binary random variable $O_t$, which we call an optimality variable, to this model where $O_t = 1$ denotes that time step $t$ is optimal, and $O_t = 0$ denotes that it is not optimal.

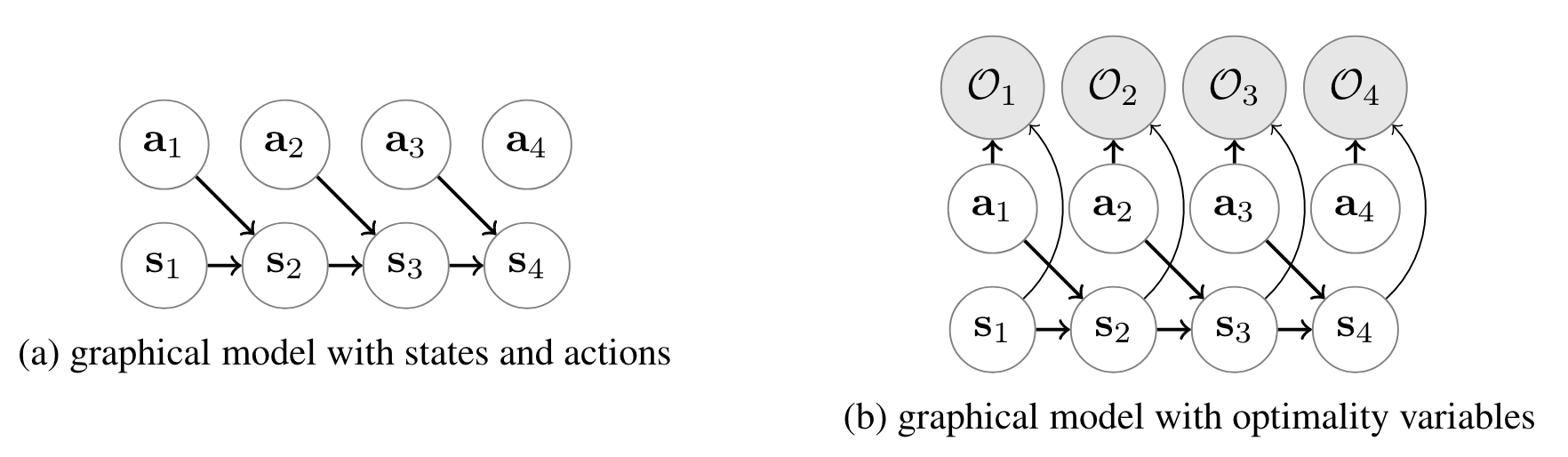
We will choose the distribution over the optimality variable as such:

$\textcolor{blue}{\underbrace{\textcolor{black}{p(O_t = 1 \mid s_t, a_t)}}_{\text{Unnormalized probability of timestep } t \text{ being optimal}}} = \textcolor{red}{\underbrace{\textcolor{black}{\exp(r(s_t, a_t))}}_{\text{proportional to the Exponent of the reward}}}.$

This seems a bit arbitrary; why are we taking the exponent of the reward?

This form resembles the Boltzmann distribution in statistical mechanics, where probabilities are proportional to $\exp(-E / T)$, with $E$ as energy and $T$ as temperature. Similarly, in reinforcement learning (RL), the reward $r(s_t, a_t)$ plays a role analogous to negative energy, and taking $\exp(r(s_t, a_t))$ ensures that higher rewards correspond to higher probabilities.

What this is really trying to get at is this — If $p(O_t = 1 \mid s_t, a_t)$ represents the probability that time step $t$ is optimal, then the reward $r(s_t, a_t)$ can be interpreted as a log-probability:

$\log p(O_t = 1 \mid s_t, a_t) \propto r(s_t, a_t).$

Exponentiating this ensures that the probabilities are normalized and non-negative. This approach is consistent with softmax-based action selection in RL, where the probability of choosing an action is proportional to $\exp(r(s_t, a_t))$. It allows smooth exploration by providing a probabilistic weighting over possible actions.

Planning = Inferring the optimal trajectory

From our PGM formulation with the optimality variable, we can infer the posterior probability of observing a trajectory given optimality for all steps in the trajectory. Given a policy (we haven’t optimized the policy parameters yet), if we would like to plan for an optimal action sequence starting from some initial state $s_1$, we can condition on $o_{1:T}$ and choose $p(s_1) = \delta(s_1)$. In other words, maximum a posteriori inference corresponds to a kind of planning problem!

$\begin{aligned} \fcolorbox{blue}{white}{$p(\tau \mid o_{1:T})$} &\propto p(\tau, o_{1:T}) \\ &= p(s_1) \prod_{t=1}^T p(O_t = 1 \mid s_t, a_t) p(s_{t+1} \mid s_t, a_t) \\ &= p(s_1) \prod_{t=1}^T \exp(r(s_t, a_t)) p(s_{t+1} \mid s_t, a_t) \\ &= \fcolorbox{green}{white}{$p(s_1) \prod_{t=1}^T p(s_{t+1} \mid s_t, a_t)$} \fcolorbox{red}{white}{$\exp \left( \sum_{t=1}^T r(s_t, a_t) \right)$}. \end{aligned}$

• Probability of observing a given trajectory given that all steps are optimal: $\textcolor{blue}{p(\tau \mid o_{1:T})}$.
• Probability of trajectory occurring according to the dynamics: $\textcolor{green}{p(s_1) \prod_{t=1}^T p(s_{t+1} \mid s_t, a_t)}$.
• Exponential of the total reward along the trajectory: $\textcolor{red}{\exp \left( \sum_{t=1}^T r(s_t, a_t) \right)}$.

* We are not directly concerned with the marginalization; instead, we want the unnormalized joint probability.

In the case where the dynamics are deterministic, the first term is a constant for all trajectories that are dynamically feasible. $p(\tau \mid o_{1:T}) \propto \fcolorbox{red}{white}{$\mathbb{1}[p(\tau) \neq 0]$} \exp \left( \sum_{t=1}^T r(s_t, a_t) \right).$ Here, the indicator function simply indicates that the trajectory $\tau$ is dynamically consistent (meaning that $p(s_{t+1} \mid s_t, a_t) \neq 0$) and the initial state is correct. So the probability of a trajectory occurring given all steps optimal is exponentially proportional to the sum of the rewards. In other words, the trajectory with the highest cumulative rewards would likely be the optimal trajectory, which is exactly what we want.

Recovering the Optimal Policy

Now we know how to find the optimal plan given a policy. We are not done yet. Remember from equation (1) that we are trying to find the optimal policy, where the expected cumulative reward across across all possible trajectories is maximized.

Lets first start by writing the optimal action conditionals within our probabilistic graphical model. This still assumes a fixed policy that is not necessarily optimal.

$p(a_t \mid s_t, O_{t:T} = 1)$

Before we go ahead, we want to make the distinction between the optimal action conditionals and the action conditionals given the optimal policy (which is the expected outcome of a standard RL frame), as the optimal action conditional is independent of the parameter $\theta$. $p(a_t \mid s_t, \theta^*)$ Nevertheless the optimal action conditional and action conditionals given the optimal policy both aim to select actions that lead to optimal outcomes and are therefore closely related. We will continue deriving the optimal action conditional in part 3!

References

1. D. Koller and N. Friedman, Probabilistic Graphical Models: Principles and Techniques, Nachdr. in Adaptive Computation and Machine Learning. Cambridge, Mass.: MIT Press, 2010.
2. S. Levine, “Reinforcement Learning and Control as Probabilistic Inference: Tutorial and Review,” 2018.